We often hear the word “REFLECTION” in the context of looking back in our life. The word reflection is also used in religious context as an important thing in the spiritual growth.
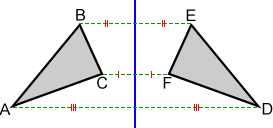
Reflection in mathematics is a fundamental concept. It refers to the flipping or mirroring of a shape, figure, or object. This happens across a specific line, known as the line of reflection. This concept is vital in understanding transformations and symmetry in geometry.

Coordinate Reflection Across Various Lines
Understanding coordinate reflection involves reflecting points across different lines in a Cartesian plane. Below is a summary of how to reflect a point (x, y) across various lines.
| Reflection Across Various Lines | Rule | Example |
|---|---|---|
| Reflection Over the X-Axis | (x, y) → (x, -y) | (4, 3) → (4, -3) |
| Reflection Over the Y-Axis | (x, y) → (-x, y) | (4, 3) → (-4, 3) |
| Reflection Over the Line y = x | (x, y) → (y, x) | (4, 3) → (3, 4) |
| Reflection Over the Line y = -x | (x, y) → (-y, -x) | (4, 3) → (-3,-4) |
| Reflection Over a Horizontal Line y = k | (x, y) → (x, 2k – y) | Over the Line y = 2 : (4, 3) → (4, 1) |
| Reflection Over a Vertical Line x = h | (x, y) → (2h – x, y) | Over the Line x = 2 : (4, 3) → (0, 3) |
Applications of Reflection
- Geometry: Used to understand symmetry in shapes and designs.
- Computer Graphics: Involves reflections for rendering images and creating visual effects.
- Art and Design: Reflective symmetry is often used in architectural designs and art.
You can also turn in to our blog for insights on Math & tutoring.
Cheers!! ❤️
