I was working with a student this week and have seen him struggling with the conversion of a decimal number into a fraction. I thought it would be a good idea to write down the process in an easy and understandable manner.
What are decimal number?
Decimal numbers are a numerical representation system commonly used in everyday life. These numbers help us to increase our accuracy and precision. Generally recognized by the “.” (dot) symbol. The dot separates the whole number part from the fractional part.
They are based on the decimal numeral system, also known as base-10, which means it uses ten symbols (0-9) to represent numbers. Each digit in a decimal number has a place value that determines its significance. For example, in the decimal number 123.45, the digit 1 represents one hundred, the digit 2 represents twenty, the digit 3 represents three, the digit 4 represents four-tenths, and the digit 5 represents five-hundredths.
Types of decimal numbers :
A) Non-Repeating and Non-Terminating decimal numbers, (also known as irrational numbers, decimal representations that neither terminate (end) nor repeat a specific pattern of digits. These numbers CANNOT BE EXPRESSED AS A FRACTION of two integers. Such as (continues indefinitely without repetition) : π (pi): approx. 3.14159265359… , √2 : approx. 1.41421356237… , e (Euler’s number): approx. 2.71828182846… , √3 : approx. 1.73205080757…
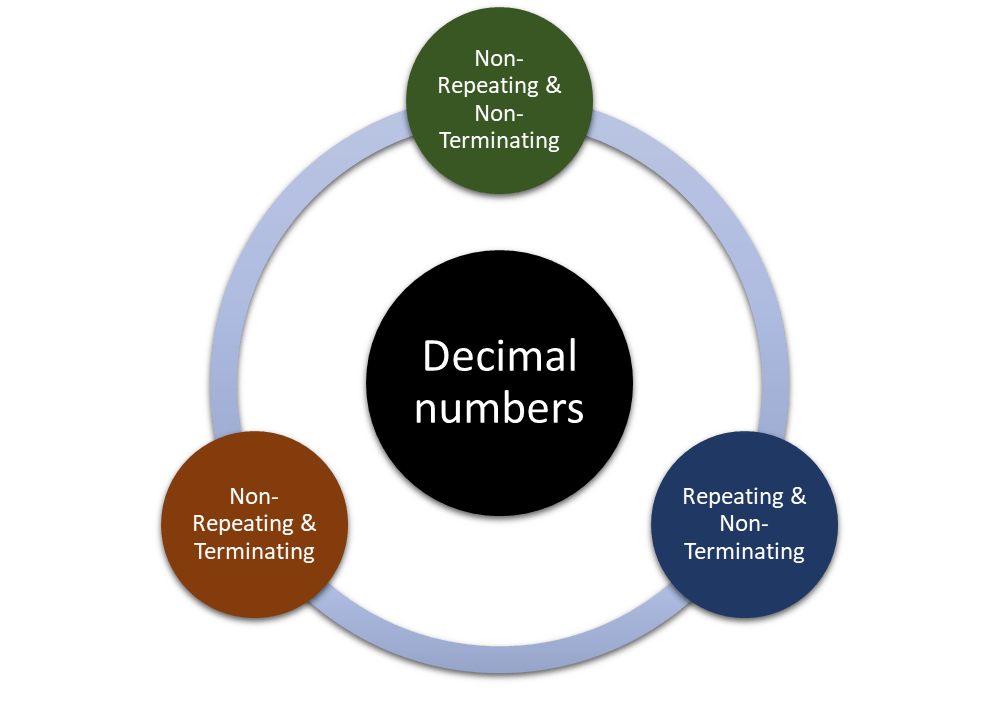
B) Non-Repeating & Terminating decimal numbers : Examples are as follow : 0.25 , 1.75 or 9.123 etc. For converting a non-repeating & Terminating decimal number into a fraction, you can follow these steps:
Step 1 : Let x be the non-repeating decimal number and count the number of decimal places in x. Let’s call it d.
Step 2: Write the number without the decimal digit and place it over a denominator of 10d (the number of decimal places).
Step 3 : Simplify the fraction and reduce it in the simplest form using prime factorization.
Here’s an example to illustrate the process:
Let’s convert the non-repeating decimal 0.75 into a fraction.
Step 1 : Set x = 0.75.
There are two decimal places in 0.75, so d = 2.
Step 2 : Write the number without the decimal point and decide it over denominator of 102. x = 75/100.
Step 3 : Reduce the fraction using prime factorization to x = 3/4.
Therefore, 0.75 can be expressed as the fraction 3/4.
C) Repeating & Non-Terminating decimal numbers : examples are 0.3333.. , 10.234234234 .. , 0.75757575.. etc.. For converting a repeating decimal number into a fraction is a bit tricky and involves multiple steps:
Step 1 : Let x be the repeating decimal number. for example –
x = 0.333… -> (Equation # 1.)
Step 2 : Identify the repeating part of the decimal. the repeating part is 3 & n be the number of digits in the repeating part. In this case, n = 1.
Step 3 : Create another equation by multiplying the equation with 10n. The equation would be
10n * x = 10n * 0. 3333…
Here, n = 1, which simplifies to
10x = 3.333… -> (Equation # 2)
Step 4 : Subtract the Equation no. 1 from Equation no. 2. This gives us
10x – x = 3.333… – 0.333…,
which simplifies to
9x = 3.
Step 5 : Solve the equation for x. Dividing both sides by 9 gives us
x = 3/9.
Step 6 : Reduce the fraction using prime factorization gives us
x = 1/3.
It is funny to see my students asking Siri or Alexa of the decimal conversion :) . I hope they enjoy it and learn the process their own rather than depending on the high-tech gadgets.
Cheers! ❤️
Subscribe To Our Blogs :
